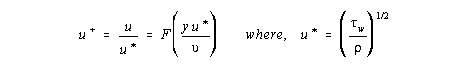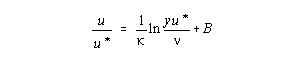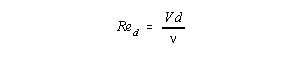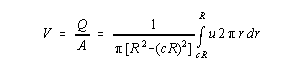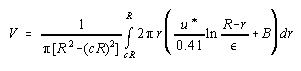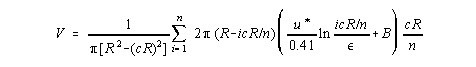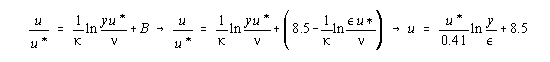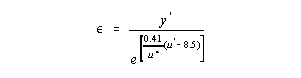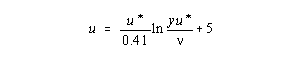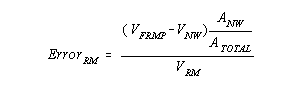Stephen K. Norfleet
RMB Consulting & Research, Inc.

Summary

Reference Method 2, which is EPA's designated standard for measuring volumetric stack flow, is biased because it does not address shear effects near stack walls. This paper discusses wall effects on stack flow velocities and compares the theoretical velocity calculations to actual near wall velocity measurements. The theoretical approach is then used to determine the extent of the overestimation bias in Method 2 due to wall effects across a wide range of applicable utility stack configurations. The wall effect related overestimation associated with 16-point velocity traverses ranges from about 1.7% to 3.0% with a mean value of about 2.2%. At a SO₂ allowance cost of $150/ton, the overestimation associated with wall effects represents an economic impact in excess of a quarter billion dollars for the utility industry during the next decade alone. The impact may be even greater when other issues affected by stack flow measurements are considered.

Background

Under the Acid Rain Program, utilities have been required to install continuous emission monitoring systems (CEMS) in order to measure, among other things, SO₂ emissions from nearly all fossil fuel-fired generating units. The SO₂ emission measurements are then reconsiled against allowances apportioned to utilities in accordance with 1985 emissions. The allowances, which may be traded among utilities, cap nation-wide SO₂ emissions at 8.9 million tons per year beginning in 2000. This emissions accounting framework conveys a monetary value to CEMS data and necessitates precise, accurate measurements.

For most units, particularly coal-fired units, SO₂ emissions are determined using a combination of a SO₂ concentration monitor and a volumetric stack flow monitor. Emissions are calculated in accordance with the following equation:

E_h = K C_S Q_h

where,

E_h = hourly SO₂ emissions, lb SO₂/hr

K = 1.66 x 10^-7 for SO₂, (lb/scf)/ppm

C_S = average hourly SO₂ concentration, ppm

Q_h = hourly flue gas flow rate, scfh

From the equation, it can be seen that any bias in the stack flow measurement will introduce a bias of equal magnitude in the calculated SO₂ emissions. One source of bias is the equal area traverse procedure defined in Method 1 that is used in conjunction with Method 2, EPA's standard measurement method (i.e., reference method) for stack volumetric flow rate. Since Methods 1 and 2 are used not only to certify, but also to calibrate CEMS flow monitors, any bias in Methods 1 or 2 will be transferred to the stack flow monitors.

The equal area traverse procedure in Method 1 introduces a bias in the reference method because it does not account for shear effects which take the stack velocity to zero at the wall. Equal area traverses assume that the average flow for a given area in the stack is represented by the flow measured at the centroid of that area. While this is essentially true for the central regions of the stack, it is not correct for the areas nearest the stack wall. Such an assumption invariably results in an overestimation of the actual average velocity because it neglects the significant velocity "drop off" as the velocity approaches zero at the wall.

Because the Acid Rain allowance program is dependant on precise, quantifiable emissions measurements, an inherent bias, such as the one introduced by equal area traverses, should be, if possible, be eliminated. Such a bias is incompatible with the concept of emission caps and trading. An adjustment for wall effects, therefore, should be allowed and, as a matter of practicality, should be as simple to implement as possible.

Theoretical Evaluation of Wall Effects⁽¹⁾

Figure 1 shows the typical velocity and shear stress distributions near a wall. The figure shows that there are three regions in turbulent flow near a wall:

1) A wall layer where viscous (laminar) shear dominates

2) An outer layer where turbulent shear dominates

3) An overlap layer where both turbulent and viscous shear are important

In 1930, Prandtl deduced that velocity in the wall layer is independent of the shear-layer thickness and can be represented as a function of kinematic viscosity, wall shear, fluid density and the distance from the from the wall. Based on dimensional analysis, one can derive the function known as the law of the wall:

[The quantity u^* is called the friction velocity because it has the same dimensions as velocity although it is not actually a flow velocity.]

In 1933, Kármán found that the difference between the velocity in the outer layer and the velocity at the edge of the shear layer is independent of viscosity but is related to shear layer thickness. In accordance with dimensional analysis, this relationship can be rewritten as the following equation known as the velocity-defect law:

Both the wall law and the defect law have been demonstrated to be accurate over a wide variety of turbulent duct flows. Intuitively, the two different laws must overlap smoothly in the intermediate layer. C. B. Millikan, in 1937, showed that overlap-layer velocity varies logarithmically with the distance from the wall:

where 0.41 and B is dependent on wall roughness. For hydraulically smooth walls (u^*/<5), there is no effect of roughness and B = 5.0. For fully rough flows (u^*/<70), the sublayer is totally broken up and B = 8.5-(1/k)ln(eu^*/v), causing the viscosity term to vanish in the logarithmic law; hence, the relationship is independent of Reynolds number for fully rough flows.

The three laws (wall law, defect law and the logarithmic overlap layer equation) are illustrated in Figure 2. The correlation of velocity profiles in the figure serves as the basis for existing turbulent-shear flow "theory." The wall law only applies to about y⁺ = 5 where it begins to merge with the logarithmic law. (The wall law region represents less than a tenth of an inch in a typical utility stack.) The most useful relationship of the three is the logarithmic law, which more than just being a mere overlap link, nearly approximates the entire velocity profile.

Applying the Logarithmic Law to Utility Stacks

The logarithmic law can be applied to utility stacks since all stack flows (at or above minimum normal load) easily fall within the classification of turbulent flow. Turbulent flow is defined in accordance with Reynolds number:

where,

Re_d = Reynolds number, dimensionless

V = Average stack velocity, ft/s

d = Stack diameter, ft

v= kinematic viscosity, ft²/s

The transition from laminar to turbulent flow occurs at Reynolds numbers of about 2300. Reynolds numbers for utility stacks typically range from about 1,000,000 to 10,000,000 -- very clearly indicating turbulent flow.

The total flow in the region from the test point measurement nearest the wall to the wall can be calculated by integrating the logarithmic law around the axis of the stack. The total near wall flow can be translated into an average velocity by dividing it by the area of the near wall region.

For circular stacks⁽²⁾:

where,

c = the fractional portion of the stack radius represented by the distance between the test point nearest the wall and the wall

R = stack radius

u = stack velocity as a function of r, where r is the distance from the center of the stack

Introducing the logarithmic law and noting that y = R - r:

Alternatively, the near wall average velocity can be approximated using a Riemann Sum technique:

For this report, the logarithmic law model was used in conjunction with a numerical integration technique employed by EPA in its recent volumetric stack flow measurement field test work⁽³⁾. The EPA technique is similar, although not identical to the Riemann Sum approach shown above. Using the procedure defined in the EPA field test plan, flow measurements are taken at one-inch intervals out to either 18 inches or the boundary of the Method 1 equal area nearest the wall. If the boundary of the Method 1 equal area nearest the wall is further than 18 inches from the wall, a measurement at the centroid of the area between the point 18 inches from the wall is taken as representative of the remaining area to the boundary. The model was used to simulate measurements at the prescribed points. These values were used along with the numerical integration technique in EPA's field test plan to calculate model-based wall effects bias values, correction factors values, and average near wall velocities found herein.

The EPA numerical integration technique was simply used as a matter of convention to help maintain consistency when comparing the results of this report with those presented in EPA field test results. While employing the EPA technique does not take full advantage of the potential resolution offered by the model⁽⁴⁾, the EPA technique is certainly an adequate approach for determining the bias associated with wall effects

While the logarithmic law could be used to approximate the flow profile across the entire stack, it is most appropriate for a range of about y⁺=10 to about y⁺=10⁴ (see Figure 2). This, fortunately, coincides with the region where the flow measurements nearest the wall are prescribed by Method 1⁽⁵⁾. The availability of a measurement in this region allows for very accurate characterization of the near wall velocity profile.

Rough Wall Application

In addition to well defined turbulence, the vast majority of utility stacks display characteristics of fully rough flow. This fully rough flow is a result of the high stack velocities coupled with the low flue gas viscosity and the fact that stacks are typically lined with very rough materials such as crudely mortared brick or various applied synthetic materials. The typical range of u^*/v for a utility stack is about 150-2000, which is significantly greater than the accepted threshold of 70 at which the sublayer is considered to be totally broken up; thus B = 8.5-(1/k)ln(eu^*/v) should be used with the logarithmic law. Fortuitously, this simplifies the equation since the viscosity term essentially disappears making the relationship Reynolds number independent:

The most difficult aspect of applying the logarithmic law model is determining the stack roughness. Stack roughness is often difficult to estimate due to the non-uniform nature of the stack surface. Roughness can also be a somewhat localized phenomenon, effected by disturbances or surface abnormalities near the sampling ports. Fortunately, the model itself can be used to calculate the roughness by rearranging the logarithmic law equation to determine the stack roughness based on a single measurement near the port, ideally the nearest wall measurement (e.g. one inch from the wall):

where,

u = velocity of near wall measurement

y = distance from wall of near wall measurement

Smooth Wall Application

A common exception regarding stack roughness would be steel stack liners used for many gas-fired units. While most units with steel-lined or other hydraulically smooth stacks walls (u^*/<5) do not require stack flow measurements, some coal-fired applications do fall under the smooth stack classification. For hydraulically smooth stacks, the near wall velocity can be determined using the following form of the logarithmic law equation:

Unlike for rough walls, the near wall velocity profile for smooth stacks is not Reynolds number independent. The near wall is subject, albeit only slightly, to variation of the average stack velocity and flue gas kinematic viscosity, which varies with flue gas temperature.

Comparison of Logarithmic Overlap Law with Actual Near Wall Measurements

The effectiveness and accuracy of the logarithmic overlap law has been firmly established and tested over a wide range of conditions during the past 60 years. Nevertheless, a comparison of the results of the logarithmic overlap law model with actual near wall measurements taken at various utility stacks, representing both EPRI and EPA flow study field test sites, is presented in this section. Data from both smooth and rough wall stacks are presented. These data are offered for illustrative purposes to demonstrate the effectiveness of the logarithmic overlap law model and help build confidence in its ability to accurately predict the actual near wall profiles for utility stack applications⁽⁶⁾. The data from the following utility stacks are presented in this section:

Smooth Stacks (Click on the unit name to view the graph for each unit)

Rough Wall Stacks (Click on the unit name to view the graph for each unit)

^*Nameplate Capacity

The tests data shown in this section represent typical full to normal load operation, with the exception of the test data for Mitchell where the unit was operated at low load levels during tests. Only test data collected under stable operating conditions are presented⁽⁷⁾. Since most of the wall effects data from the EPA test study were collected using an automated S-type probe, for consistency's sake, only the data collected using the automated probe is presented for the EPA tests. For the sake of economy, while more than one stable load test may have been performed at each site, only one representative test is shown graphically for each site.

In the figures, the results of the logarithmic overlay law were calculated using the velocity value for the standard traverse point nearest the wall as the initial "reference point" used to determine the friction velocity, u^*. For the rough wall stacks, the calculated flows were also based on a stack roughness factor determined using the flow measurement nearest the wall, typically one inch from the wall, in conjunction with procedure previously described.

As Figures 6-10 show, the near wall measurements compared very well with the logarithmic overlay law model calculated velocity profile. While the discrepancies between the calculated and measured values were very small for all units, the discrepancies at Titus and Picway were somewhat greater than the others. At Titus and Picway, the wall effects appeared to be significantly greater at one port with respect to that measured or modeled at the other ports (Titus - Port D; Picway- Port C). This apparent difference suggests that wall effects should be either measured or modeled for each port to adequately assess the true overestimation bias. [The apparent port-to-port differences at Titus and Picway could have, alternatively, been caused by probe mispositioning or flow disturbances. The Titus data also reflects only marginal stabile conditions.]

Reference Method Flow Overestimation Due to Wall Effects

The logarithmic overlap law can be used to determine the amount of bias in the stack flow reference method due to wall effects. Again, this bias is due to a lack of correction for the velocity "drop off" in equal area traverse averaging. The wall related overestimation error in the reference method can be calculated as follows:

where,

Error_RM = Overestimation bias in the flow reference method due to a lack of wall effect compensation, %

V_FRMP = Average measured velocity at test points nearest the wall, ft/s

V_NW = Average velocity in the near wall area calculated using the logarithmic law, ft/s

V_RM = Average (total stack) reference method velocity, ft/s

A_NW = Near wall stack cross-sectional area (from nearest test point to the stack wall), ft²

A_TOTAL = Total stack cross-sectional area, ft²

While the wall effects for stacks with the same characteristics (i.e., wall roughness, stack diameter, etc.) will be the same, the overestimation error may not. This is because, in addition to the actual viscous shear related wall effects, the overestimation error is also dependant on the shape of velocity profile across the stack. Two identical stacks with equal flow may have differing flow profiles due to non-uniform flow (See Figure 12).

To account for varying flow profiles and present the data in a more universal format, the preceding error equation can be rewritten in terms of a velocity profile ratio, R_VP defined as V_FRMP/V_RM:

By defining the overestimation bias in terms of the velocity profile ratio, the wall effects related bias can be determined based on the stack conditions for a velocity profile ratio = 1, and those values can easily be converted to a given velocity profile by multiplying tabulated error times the actual velocity profile ratio⁽⁸⁾.

Another influence on the overestimation bias associated with the stack flow reference method is the number of velocity traverse points used. The overestimation increases as the number of traverse points are reduced and decreases when the number of traverse points are increased. For example, the overestimation bias associated with a 12-point velocity traverse is about 30% greater than that for a 16-point traverse. The overestimation bias for a 20-point traverse is about 15% less than that for a 16-point traverse.

For rough stacks, the logarithmic overlap law was used to create the matrix shown in Table 2. As discussed in a previous section, for rough walled utility stacks, the logarithmic overlap law is independent of Reynolds number. In practical terms, this means that the wall effects are independent of velocity and viscosity. Only wall roughness and stack diameter remain as influences. Table 2 presents reference method wall effect bias representative of a wide range of utility stack diameters and wall roughness values for a for a velocity profile ratio = 1. Table 2 shows the reference method wall effect bias associated the use of 16 velocity traverse points, the minimum number of points required in Method 1 for many applications. The stack diameter and roughness values in the table were selected to represent the typical utility stacks where flow monitors and Method 2 are applied for coal-fired and some oil-fired units. Correcting the rough wall effects to reflect a typical velocity profile ratio of 0.90, with 16-point velocity traverse, the overstatement ranges from about 1.7% to 3.0% with a mean value of about 2.2% for circular stacks with diameters of 10 to 35 ft. and roughness values of 0.02 to 0.10 ft.⁽⁹⁾.

Table 2. Rough Wall Reference Method Overestimation Bias Due to Lack of Wall Effect Correction (16 Traverse Points, R_VP=1)

Table 3 shows the wall effect related bias calculated using the logarithmic overlap law for smooth stacks. Unlike for rough walled stacks, the logarithmic overlap law for smooth stacks is dependent, albeit only slightly, on Reynolds number.⁽¹⁰⁾ As shown in Table 3, the wall effect related bias only decreases by about 0.01% to 0.2% per 10 aft/s increase in velocity over the 40 to 100 aft/s range.⁽¹¹⁾ The effect of kinematic viscosity, which is a function primarily of stack temperature, is likewise small. The wall effect related bias increases by only about 0.01% with a corresponding 100F increase in temperature over the 150F to 700F range. Table 2 presents reference method wall effect bias representative of a wide range of utility stack diameters and wall roughness values for a velocity profile ratio = 1.

Table 3. Smooth Wall Reference Method Overestimation Bias Due to Lack of Wall Effect Correction (16 Traverse Points, R_VP=1, 300F)

Conclusions and Recommendation

At a SO₂ allowance cost of $150/ton, the wall effects related overestimation bias represents an economic impact in excess of a quarter of a billion dollars for the utility industry during the next decade alone. The impact maybe even greater when other issues affected by flow measurements, such as NO_X budget, PM standards, and possible permit limitations, are considered.

Since the allowance program is dependant on precise, quantifiable emissions measurements, an inherent bias, such as the one introduced by equal area traverses, should be eliminated. Such a bias is incompatible with the concept of emission caps and trading. An adjustment for wall effects should, therefore, be allowed and, as a matter of practicality, should be as simple to implement as possible.

Because, for rough stacks, wall effect overestimation bias is related only to stack diameter and wall roughness factors which do not change appreciably over time as long as no stack modifications are made, a one-time wall effect correction could be determined and applied to subsequent stack flow reference methods test. The same principle could be applied to smooth stacks since the effect of Reynolds number is essentially negligible for these stacks as well. This one-time value could be corrected based on the number of test points used for a given reference method test. Corrections for the velocity profile ratio could be performed whenever a relative accuracy assessment is done but seem unnecessary since the flow profile would likely remain the same for a given unit at the same approximate load.

An intensive measurement-based wall effects correction could certainly be used to provide a correction factor for the equal area traverse overestimation bias. But, requiring a significant number of additional stack flow measurements, such as the 96 additional measurements that would be required for most units per the near wall procedures included in EPA's flow measurement study field test plan, would be costly and are unnecessary. Numerical integration techniques would also introduce added complexity to the method which could lead to a greater level of miscalculations when correction factors are determined.

The logarithmic overlap law provides an simple, accurate, cost effective technique for determining correction factors to compensate for the inherent wall effects bias in the stack flow reference method. For smooth stacks, the technique requires no additional measurements. For rough wall stacks, which represent the vast majority of applicable stacks, one additional near wall measurement would be required at each port in order to assess the wall roughness. Values could be calculated using either the logarithmic law model itself or could be determined from a table such as the ones presented in this report.

For greater simplicity, in addition to determining the correction factor using the model or a table, utilities should also be given the option to choose a default correction factor. This default correction factor, which would be similar in concept to the default Pitot coefficient included in Method 2, would represent a conservation approximation of the mean correction factor for utility stacks and would streamline the process for utilities. In accordance with the results of this study, default correction factors of 2.0% (0.98) for rough-walled stacks and 1.50% (0.985) for smooth-walled stacks would be appropriate.

Endnotes

1. This section summarizes information contained in Chapter 6 from White, Frank M. Fluid Mechanics. 2nd ed., McGraw-Hill, New York. 1986.

2. This report focuses on wall effects for circular stacks only. While much of the information presented herein also applies to rectangular ducts, the special considerations associated with measuring and modeling near wall velocities in rectangular ducts was beyond the scope of this study. Further investigation is warranted in this area.

3. During 1997, EPA conducted a series of field tests to evaluate potential modifications to its volumetric stack flow measurement methods.

4. Using greater resolution, i.e., more than 18 data points, would result in slightly higher "average" near wall velocities.

5. This "coincidence" provides an explanation that accounts for the fact that the test point nearest the wall tends to fall near the beginning of the "dip" in the velocity profile since the point represents the transition between the outer law profile and the logarithmic overlap area.

6. Points beyond the standard traverse point nearest the wall tend to fall outside the actual logarithmic overlap area where the accuracy of the logarithmic law is best. To enhance accuracy, the model velocities shown in the figures and used to calculate overestimation bias were interpolated from the standard traverse data for points from the first traverse point to the boundary of the equal area region.

7. Maintaining stable conditions is critical when attempting to measure wall effects since the effect itself has a magnitude of only about 2% of the total flow.

8. The velocity profile ratios for smooth stacks tend to be higher than those for rough walls. The velocity profile ratio also tends to be higher for larger diameter stacks, since there is a greater impact of wall effects on the closest traverse point to the wall for smaller stacks. For Decordova, Lake Hubbard, and Homer City, the velocity profile ratios corresponding to the wall effects example data presented in this report were 0.97, 1.09 and 0.96, respectively. For the rough wall examples, the velocity profile ratios ranged from 0.82 to 0.96 with an average of about 0.90.

9. Test data suggest that the average effective wall roughness may be significantly greater than 0.10 ft. for some stacks.

10. Correspondingly, no discernable Reynolds number effect was observed from the EPRI or EPA tests done at either the smooth or, as expected, rough wall sites.

11. The relationship of wall effects to changes in velocity is more significant for velocities less than 30 aft/s.

Agora Environmental Consulting
Last Revised: February 25, 2008